De ronding

Wat is nu eigenlijk de juiste ronding?

Wat is nu eigenlijk de juiste ronding? Hiervoor moeten we eerst kijken naar een belangrijke eigenschap van ijs. Het volume van ijs is groter dan het volume van water (bij hetzelfde gewicht van de stof). Met andere woorden. wanneer ijs melt ‘krimpt’ de stof. Wat gebeurt er nu bij het schaatsen? Het gewicht van een schaatser oefent via de schaats een druk uit op het ijs. Het ijs wordt samengeperst en bij voldoende druk wordt dit ijs water. Je schaatst dus eigenlijk niet op ijs, maar op een dun laagje water. Dat dit goed glijdt, kun je aan iedere automobilist vragen die weleens te maken heeft gehad met aquaplaining.

Dame op hakken

Dame op hakken Om nog even aan te geven dat de druk, die uitgeoefend wordt op het ijs groot is, kunnen we zien aan de volgende eenvoudige berekening: Stel het draagvlak van een schaats is 2 cm bij 0.1 cm, is het oppervlak dus 0.2 cm² . Wanneer de schaatser 70 kg weegt is de druk gelijk aan 70 kg / 0.2 cm²= 350 kg per vierkante cm. Dit is per vierkante meter 3500 ton. Je kunt hiermee bewijzen dat je moeder met naaldhakken meer kg / m2 druk veroorzaakt als een olifant met platte poten. (doe hier wel heel voorzichtig mee, en laat het anders aan je vader over!!!!).

Uit bovenstaande berekening is duidelijk te zien dat de druk die uitgeoefend wordt op het ijs te regelen is d.m.v. de grootte van het ijzer oppervlak wat zich op het ijs bevindt. De oppervlakte grootte hangt dus nauw samen met de ronding van de schaats. Hoe vlakker de schaats des te meer oppervlakte ijs wordt er bestreken. Hieruit kan direct of indirect worden afgeleid dat de grootte van de ronding afhangt van de volgende factoren:

Het gewicht van de schaatser. Hoe groter het gewicht des te vlakker moet de schaats zijn.
De ijstemperatuur. Hoe lager de ijstemperatuur des te sterker is de structuur vandaar een rondere schaats.
De smaak van de rijder. Een wendbare schaats is ronder.

Er zijn nog meer redenen waarom schaatsen glijden. Hier kan de wrijvingswarmte genoemd worden, hoewel deze bijdrage voor wat betreft het smelten bijzonder klein is. IJzer geleidt namelijk warmte beter als water (ijs) zodat de eventuele ontstane warmte eerder door het ijzer wordt afgevoerd als door het ijs. Een nieuw gevonden reden van het glijden op ijs, las ik in de schaatskroniek (23ste jaargang nr l). Het wordt de grenslaag theorie genoemd. Bij de overgang van ijs naar lucht zijn bepaalde eigenschappen te ontdekken. Ik citeer: Door bepaalde thermodynamische processen ontstaan er aan de oppervlakte van het ijs een speciaal soort bindingen tussen de ijsmoleculen, waarvan de structuur min of meer vloeibaar is. Deze vloeibaar lijkende laag kan goed dienen als smeermiddel tussen schaats en ijs. De dikte van deze laag wordt dunner bij het afnemen van de ijstemperatuur. Bij een ijstemperatuur van -5 graden Celcius is het laagje enkele tientallen moleculen dik. Uit de smerings-theorieën is bekend, dat in sommige gevallen een laagje smeermiddel van twee moleculen dik al voldoende is de wrijvingsweerstand flink te laten dalen. Verder wordt in het artikel, wat ik sterk aanraad om ook te lezen, gesproken over een rolletjes structuur. De moleculen die zich bevinden op de eerdergenoemde grenslaag vormen een soort rolletjes. Hetzelfde idee als knikkers op een betonnen vloer.

De ronding van de schaats

De ronding van de schaats Al met al doen bovengenoemde theorieën niet af aan de eerder genoemde drie stelling. En om wat duidelijker te zijn over de ronding volgen hier wat cijfers. De ronding van een schaats wordt vaak uitgedrukt in de lengte van de straal van een cirkel waarin de schaats past (zie figuur boven).

In sommige boeken (b.v. in “Schaatsen” van Jos Geijsel) wordt gesproken over een straal van tussen de 21 meter en 24 meter. Iets wat mij een erg vlakke ronding lijkt (later in het eerder genoemde boek spreekt de schrijver zichzelf dan ook tegen). Na wat gesprekken met anderen, blijkt de straal (naar mijn idee) te liggen tussen de 16 en 19 meter (Op Nederlands ijs onder normale weersomstandigheden).

Maar hoe kun je de straal nu meten? Om de straal van een cirkel te bepalen heb je drie punten nodig. Het eerste meetpunt is het zwaartepunt van je schaats. Dit is de plaats waar het ijzer het ijs raakt en bevindt izch op eenderde deel van de totale afstand tussen potten gemeten van de achterpot (zie hiervoor onderstaande tekening). Het tweede en derde meetpunt is de voor- en achterkant van de schaats. Het achter meetpunt ligt 15 cm van het zwartepunt. Het voormeetpunt ligt op 20 cm van het zwartepunt. De drie meetpunten zijn ook in de tekening weergegeven.

Plaats van het zwaartepunt

Plaats van het zwaartepunt 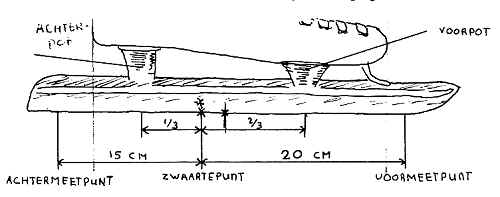Na het afzetten van deze drie punten op de schaats kan er gemeten worden. Een metalen rij (lineaal) wordt tegen het zwaartepunt gehouden. Aan de voor- en achterzijde ontstaat nu een luchtspleet tussen ijzer en rij. Door nu de grootte van deze luchtspleet te meten op de twee resterende meetpunten kan vervolgens worden afgelezen uit de onderstaande tabel wat de straal van de cirkel is.

Straal	voor	achter
12 mtr	1.6 mm	1.0 mm
13 mtr	1,5 mm	0.9 mm
14 mtr	1.4 mm	0.8 mm
15 mtr	1.3 mm	0.7 mm
16 mtr	1.2 mm	0.7 mm
17 mtr	1.1 mm	0.6 mm
18 mtr	1.0 mm	0.6 mm

Het is niet de bedoeling dat iedereen nu zijn schaatsen gaat zitten slijpen om een juiste ronding te verkrijgen, maar meer om een idee te geven waarom zit er een ronding in m’n schaatsen en hoe groot moet deze ongeveer zijn. Wel hoop ik, dat ik d.m.v. dit verhaal heb kunnen bijdragen aan een nog betere conditie van je schaatsen. De in de tekst genoemde ronding groottes berusten op ervaringen van anderen. Wanneer er mensen zijn die het er niet mee eens zijn of dat bovenstaande onvolledig is stuur gerust een bericht, wellicht kan bovenstaande tekst dan nog vollediger worden.